Kalian tau tidak mengenai bapak Phytagoras? Ga mungkin dong kalian ga pernah denger ya ga? Teorema Phytagoras digagas oleh si bapak ini lho.
Konsep Teorema Phytagoras
Phytagoras berasal dari nama seorang filsuf dan ilmuan matematika yang berasal dari Yunani Kuno pada masa 570-495 SM di kepulauan Samos.
Phytagoras yang membawa pengetahuan ini ke peradaban Yunani Kuno serta telah membuktikannya secara sistematis. Oleh karena itu, nama Phytagoras diabadikan sebagai nama dari teorema ini.
Bayangkan aja di tahun itu Mesir sudah bisa membangun piramida. Kira-kira mereka tau darimana coba kalo bukan dari ilmu ini?
Erat kaitannya dengan bangun segitiga, konsep ini khusus berlaku untuk segitiga siku-siku saja. Kalian tau nggak segitiga siku-siku itu yang gimana sih? Hayo coba diingat-ingat lagi ya!
Teorema pythagoras berbunyi:
“Di dalam sebuah segitiga siku-siku diberlakukan kuadrat dari sisi miring sama dengan jumlah kuadrat dari sisi-sisi lainnya”.
Hanya untuk segitiga siku-siku dan minimal 2 sisinya dapat diketahui terlebih dahulu.
Salah satu cirinya adalah besar sudut sikunya ada yang 90o. Kalau kalian masih belum ada bayangan sini mimin kasi gambarnya ya!
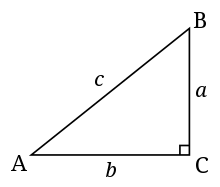
Look at that picture everybody! BC membentuk sudut siku-siku yang kalau kalian cek itu besarannya 90 derajat yes. Sisi c merupakan sisi miring (hipotenusa) segitiga siku-siku yang mana untuk menemukannya kita perlu menjumlahkan kuadrat di sisi-sisinya.
Mengapa kalian perlu memperhatikan dan memahami bentuk sebuah segitiga siku-siku? supaya apabila segitiga siku-siku nya di balik atau diganti namanya kalian tidak akan bingung.
Rumus
a (kuadrat) + b (kuadrat) = c (kuadrat)
Ternyata hanya dengan rumus ini kita bisa mengetahui jenis-jenis segitiga lho. Gimana caranya? Hmm, kalian mau tau aja atau mau tau banget nih?
a (kuadrat) + b (kuadrat) > c (kuadrat)
Jika yang terjadi seperti rumus di atas, maka segitiga itu jadinya adalah segitiga tumpul. Hehe, ternyata ada ya segitiga tumpul…
a (kuadrat) + b (kuadrat) < c (kuadrat)
Kalo rumusnya begini berarti otomatis kebalikan dari rumus sebelumnya ya. Artinya segitiga ini adalah segitiga lancip.
Contoh Soal Teorema Phytagoras
Diketahui sisi-sisi sebuah segitiga, yaitu a = 10, b = 8 dan c = 22. Dengan mengudaratkan sisi miring dan jumlahkan kuadrat sisi lainnya, maka diperoleh:
c2 = 222
c2 = 484
a2 + b2 = 102 + 82
a2 + b2 = 100 + 64
a2 + b2 = 164
Karena 164 < 484 atau a2 + b2 < c2 (102 + 82 < 222), maka segitiga ini bukan termasuk segitiga siku-siku, melainkan segitiga tumpul.
Mudah kan?
Selanjutnya, kita mau kembali ke gambar segitiga di atas dan mencari panjang AB. Jika diketahui AC 5 cm dan BC 12 cm
AC2 + Bc2 = AB2
52 + 122 = AB2
25 + 144 = AB2
169 = AB2
AB = ±√169
AB = ±13
Nah setelah tau sisi miringnya sekarang kalian bisa mencari keliling deh.
Ada juga cara triple Phytagoras supaya kalian ga repot menghitung.
Misalnya, diketahui segitiga dengan panjang sisi-sisinya, yaitu 6, 8, dan 10. Nah, menurutmu, apakah ketiga sisi tersebut merupakan triple Pythagoras?
Jawabannya, iya. Karena 6, 8, dan 10 merupakan kelipatan dari 3, 4, dan 5. Alhasil segitiga tersebut pasti merupakan segitiga siku-siku. Memang harus hafalan sih kalo ini.
Berikut ini adalah angka-angka yang disebut dengan triple phytagoras:
3,4,5
5,12,13
6,8,10
7,24,25
8,15, 17
9, 12,15
10, 24, 26
Dan seterusnya
Contoh lain:
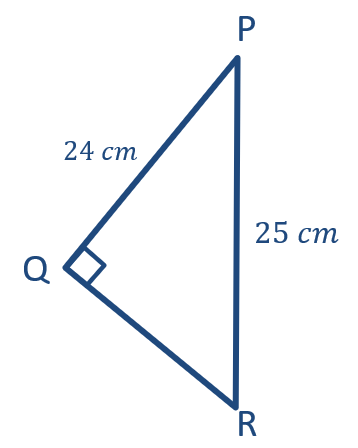
Panjang QR adalah ….
Pembahasan
Karena sudut Q merupakan sudut siku-siku, maka PR merupakan sisi miringnya, sehingga
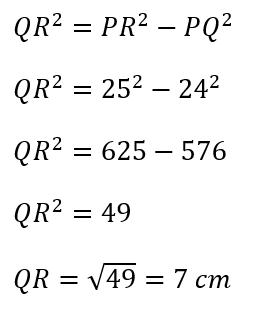
Wokai, jadi jawabannya adalah 7 ya!
Lanjut..
Suatu segitiga siku-siku memiliki sisi kemiringan sepanjang 13 cm dan alas sepanjang 12 cm. Tentukanlah berapa tinggi dari segitiga siku-siku tersebut.
Jawab:
b = 12 cm
c = 13 cm
a = ?
a2 = c2 – b2
a2 = 132 – 122
a2 = 169 – 144
a2 = 25
a = √25
a = 5
Maka tinggi dari segitiga tersebut adalah 5 cm.
Segitiga siku-siku memiliki sisi hipotenusa 10 cm dan memiliki tinggi 6 cm. Berapakah panjang dari alas segitiga siku-siku tersebut.
Jawab:
a = 6 cm
c = 10 cm
b = ?
b2 = c2 – a2
b2 = 102 – 62
b2 = 100 – 36
b2 = 64
b = √64
b = 8
Maka panjang dari alas segitiga siku-siku tersebut adalah 8 cm.
Pak Budi berencana untuk membuat wahana perosotan untuk anaknya dengan menggunakan peralatan yang ada di rumahnya. Jika jarak tempat tujuan akhir perosotan dengan tempat untuk naik yang tersedia di rumah adalah 8 meter dan tinggi dari tempat naik atau tangga dari perosotan itu adalah 6 meter, berapakah panjang sisi miring tempat untuk perosotan itu?
Jawab
Jika digambarkan dalam bentuk segitiga siku-siku maka bentuk dari flying fox itu adalah seperti ini:
Maka dapat diartikan bahwa tangga naik sama dengan tinggi segitiga, yaitu 6 cm dan jarak sama dengan alas, yaitu 8 cm.
a = 6 cm
b = 8 cm
c = ?
c
2 = a2 + b2
c2 = 62 + 82
c2= 36 + 64
c= √100
c = 10
Maka panjang dari sisi miring perosotan itu adalah 10 m.
Setelah mendapat pencerahan dari beberapa penjelasan di atas kira-kira gimana nih Sahabat Tutorindonesia? pembahasan materi koordinat kartesius sulit ga sih? Biar makin paham materinya yuk ikutan les di tutorindonesia.co.id dijamin nilai kamu bakal meningkat drastis.
Baca juga : Super Intensif SBMPTN 2022
Referensi:
1. ruangguru.com
2. akupintar.id
3. Sampoerna Academy
